ゲーム理論における最も単純で有名な2人ゲーム（プレーヤーが2人のゲーム）。アメリカ合衆国ランド研究所のメリル・フラッド（Merrill M. Flood 1908～91）とメルビン・ドレシャー（Melvin Dresher 1911～92）が1950年に考案し、顧問のアルバート・タッカー（Albert W.Tucker 1905～95）によって定式化された。「囚人のジレンマ」の名称は、彼らの考えた次のようなストーリーに由来する。
AとBの2人が、ある共同犯罪の容疑で逮捕された。しかし有罪にするだけの証拠がなく、容疑者（囚人）たちの自白だけが頼りの検事は、次のような司法取引を各容疑者に持ちかけた……。
・2人とも自白すれば、A、Bともに懲役2年。
・2人とも黙秘すれば、A、Bともに1年間の勾留。
・Aが自白、Bが黙秘すれば、Aはすぐに釈放、Bは懲役3年。
・Bが自白、Aが黙秘すれば、Bはすぐに釈放、Aは懲役3年。
この状況は、利得行列（payoff matrix）と呼ばれる表によって、簡潔に記述することができる。プレーヤーAの戦略が左側の列、Bの戦略が上の行に書き込まれており、それぞれの結果に対応する各マスの左側の数字がプレーヤーAの利得、右側がBの利得を表す。たとえば、Aが自白してBが黙秘した場合には、Aは0、Bは－3の利得を獲得する。
利得行列の表をじっくり眺めると、各プレーヤーにとって、相手が黙秘を選んでも自白を選んでも、常に自分は自白すれば利得が高くなる、ということが分かる。このように、相手の戦略に依存しない最適戦略のことを支配戦略（dominant strategy）と言う。このゲームでは、AとBどちらの容疑者にとっても「自白」が支配戦略になっているため、彼らは（自白、自白）を選ぶことになる。2人で協力して（黙秘、黙秘）を選ぶことさえできれば、1年ずつの勾留で済むにもかかわらず、2年ずつの懲役という非効率な結果に陥ってしまうのだ。これが「ジレンマ」と呼ばれる理由である。
現在では囚人のジレンマは、タッカーらが定式化した上述のストーリーを離れて、一般に「グループ内のメンバーがお互いに協力行動を取り合えば全体にとって望ましい結果が実現するにもかかわらず、各人にとっては裏切る方が得であるため非効率な結果に陥ってしまう」ようなジレンマ的な状況を幅広く指す。プレーヤーが3人以上の場合の囚人のジレンマは、社会的ジレンマ（social dilemma）とも呼ばれる。企業間の熾烈な価格競争や、大国間の軍拡競争、共有地の悲劇（tragedy of commons）など、さまざまな現象をこのフレームワークで説明することができる。囚人のジレンマという非常に単純なゲームを通じて、個人にとって最適な意思決定が全体にとって最適な結果を導くとは限らない、という重要な教訓を得ることができる。

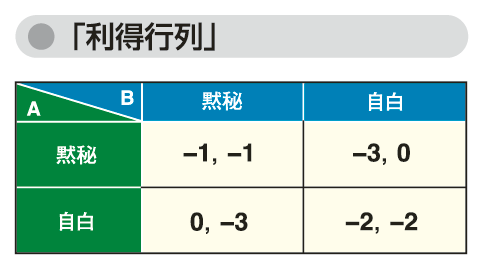
表「利得行列」