2/3や3/7のように「整数/整数」の形で表せる数を有理数という。古代ギリシャでは、数は正の有理数を指していた。有理数は負も含めると、その中で四則演算ができる完全な数でもあった。ところが、直角三角形の斜辺の長さがxで、他の2辺が1のとき、斜辺xは、
x²＝1²＋1²＝2
をみたさねばならなくなる。このxを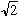と表すが、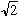は「整数/整数」の形では表せない未知の数であった。これを無理数という。この数は「線は大きさのある点の集まり」という古代ギリシャの世界観と抵触せざるをえない。無理数の発見はギリシャ数学にとって、まさしく「不祥事」だったのである。それゆえ、ピタゴラス学派はこの数の存在を隠し、「口外したものを溺死させた」という伝説もあるほどである。