図形の中の1点を固定して、その点から出てその点に戻る曲線をループ（loop）という。ループは無限にできるが、その図形の中で動かして重ねられるループを同じものと考える。この動かす操作のことをホモトープ（homotopy）という。こうした同一視によって、ループの集合には群の構造を入れることができる。これを基本群という。
円盤では、すべてのループは1点で動かないループに縮んでしまう。すなわち、基本群が単位元だけである。このような図形を単連結という。球面は単連結であるが、ドーナツの表面は単連結ではない。
さらに、四次元空間の中で同相な二つの閉曲線が、三次元空間の中では重ねられない。それは三次元空間の中の位置（position）の問題であり、これを研究するのが結び目の理論（knot theory）である。

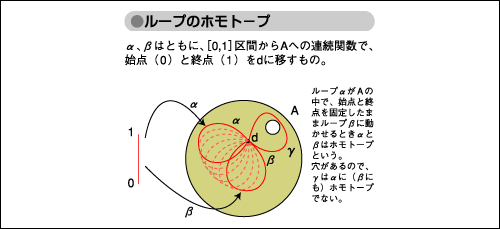
図「ループのホモトープ」

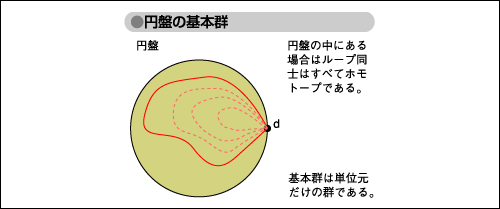
図「円盤の基本群」