異なる標本（→「統計学」）の中の位置を比べる必要が生じることがよくある。その最も典型的な例は、複数の試験で、合格者を判定する場合である。また、模擬試験で合格可能性を判定するときにもそういうことが起こる。
異なる試験で同じ70点の得点を取ったとしても、同じ成績とはいえない。まず、問題の難易度の違いがある。難易度を比較するには、平均（点）を比べるのが普通の方法である。
平均は一般に算術平均（arithmetic mean）を用い、n個のデータa₁，a₂，……，a_nについて、その平均mは次式で表される。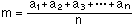

二つの標本のデータをくらべるとき、平均点の差の分だけ、低い標本のデータに加えて補正すればよいかといえば、それでも異なることがある。例えば、図「データの密集度」にあるような二つの標本の数値の平均は、同じ50である。AとBで同じ70の数値のものを比べると、Aの70のほうが標本の中で高い数値と考えられる。なぜなら、Aのほうが平均のところに多くのデータが密集し、70点より上の層が少ないからである。
このデータの密集具合、あるいはバラツキの程度を示す指標として一般に使われているのが、次式の分散Vと標準偏差σである。いずれもその値が大きくなると、データの散らばりが大きくなると判断される。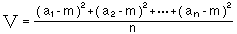


いずれも指標なので、その数値の妥当性を検証することはしない。しかし、分散よりも標準偏差のほうが、実際のバラツキの程度をよりよく示していると考えられている。

図「データの密集度」