ゆったりと伝わっていくときの波の形はかなり以前から研究されてきた。この波形は、薄い紙を巻いて斜めの平面にそって切り、これを開くことで得られる。
ロール紙の軸と平面との角度を小さくすれば、切り口は細長い楕円になるから、この波の形は上下の幅、すなわち振幅（amplitude）が大きくなる。また、ロール紙の半径が大きくなると、波の山の間隔、すなわち周期（period）が長くなり、逆にロール紙の半径が小さくなると周期が短くなる。このとき、周期はロール紙の切り口の一番高いところから次の一番高いところまでの長さとなるため、ロール紙が1周する長さといえる。つまり、ロール紙の半径が1であれば、このロール紙でできる波の形の周期は2π、ロール紙と切断する平面との角度が45°のとき、振幅が1となる。
ここで、ロール紙の側面の円周を進んだ距離をx軸にとり、切り口の高さの真ん中の点をとり、それと同じ高さの2点を結んだものを基準の軸とする。すると、波の各点の高さは基準軸からの距離と等しく（45°、90°、45°の二等辺三角形となるから）、この基準軸からの距離は、x（円の弧の長さから角度を表わす「ラジアン」という単位）のときにちょうどsin xとなる。このとき、波の曲線の高さが基準軸と交わる点の一つ（このあと高くなる点）を原点にすると、y＝sin xのグラフとなり、またこれをπ/2だけ横にずらせば、y＝cos xのグラフとなる。そのため、これらの関数を三角関数という。

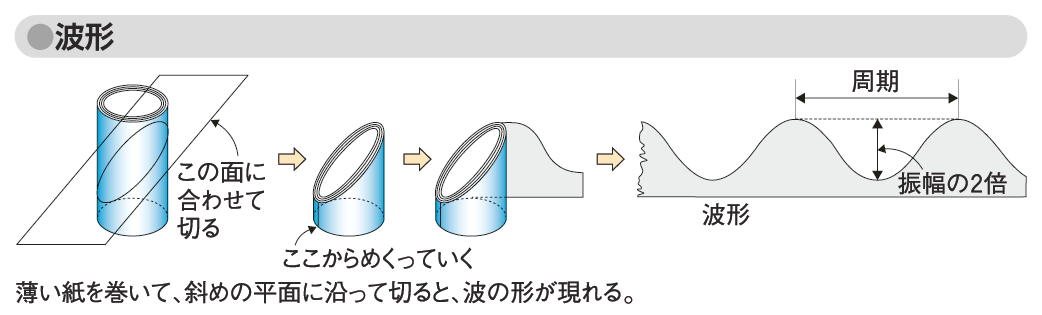
図「波形」

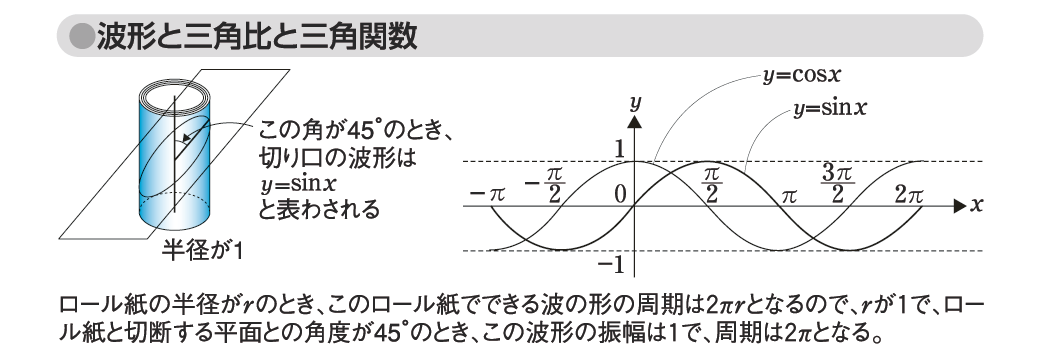
図「波形と三角比と三角関数」