円が与えられたとき、その円の中心Oと二つの半径によってできる角（普通は小さいほう）を中心角といい、円周の一部で連続した部分を円弧という。円周上の点Aから点Bまでの円弧を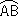と表す。この表しかたでは、普通は短いほうの円弧（劣弧　minor arc）を指すが、特に長いほうの円弧を指すときは、その円弧の1点Cを示しておいて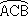と表す。
また、円周上の2点AとBを結ぶ線分を特に弦（string）といいと表す。弦の中心角は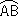の中心角とする。当然、同じ円周上の二つの弦の中心角が等しければ、弧の長さと弦の長さが等しくなる。
逆に、弧の長さ、あるいは弦の長さが等しいとき、中心角は等しくなる。
弧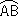（あるいは弦）に対する円周角とは、円周上の1点Pを用いて、∠APBと表される角のことであり、円周角の2倍が中心角となる。このことから、の円周角はPによらず一定であり、これを円周角の定理（inscribed angle theorem）という。
逆に、∠ACB＝∠ADBならば、4点ABDCは一つの円周上にあることになり、これを円周角の定理の逆という。
円周角の定理から、四辺形ABDCが円に内接すれば、∠A＝（180°－∠D）となり、逆も成り立つことがわかる。このことと平行四辺形の性質から、円に内接する平行四辺形は長方形に限ることもわかる。また、この結果をもとに、円に内接する四辺形ABDCのDとCを限りなく近づければ、DCを通る直線は円の接線になり、∠BAC＝∠BCPとなる。これを接弦定理（alternate segment theorem）という。

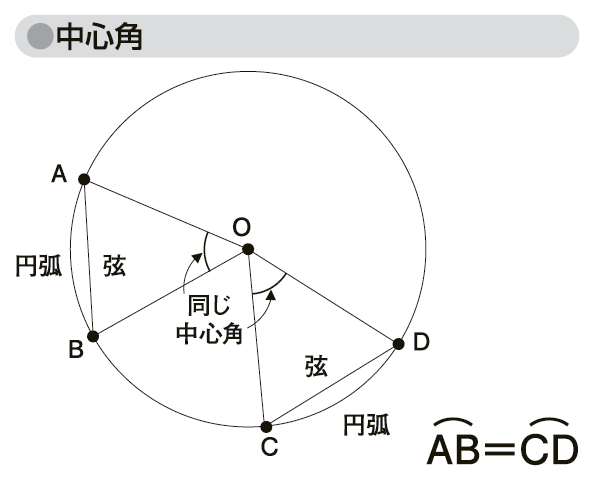
図「中心角」

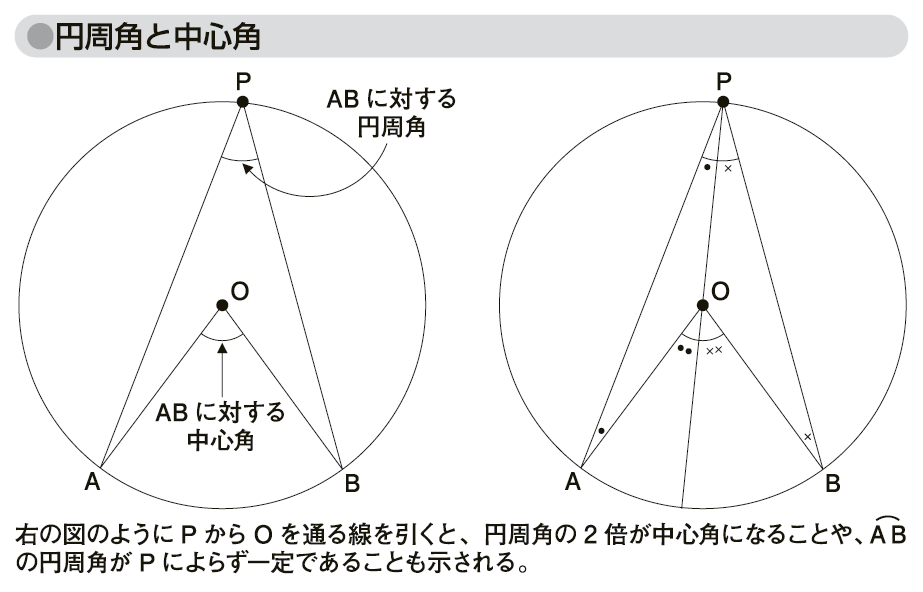
図「円周角と中心角」

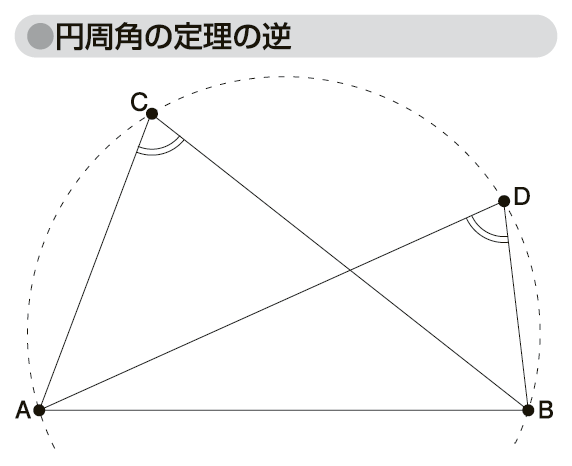
図「円周角の定理の逆」

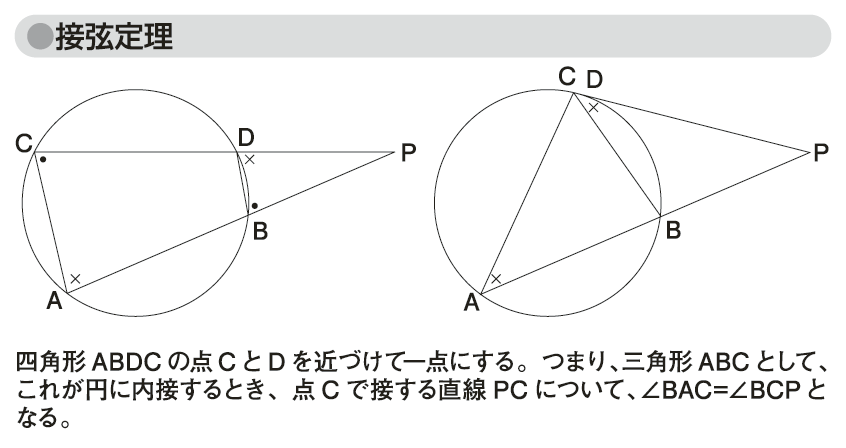
図「接弦定理」