人間の感覚の甘さを突いた図形の一つで、図形をうまく切り分け、それを組み換えたときに面積が変わってしまうという図形。たとえば、1800年代から知られ、最近ではフランス数学会の啓蒙パンフレットにも使われていた図がある。まず、縦5cm、横13cmの長方形を用意する。その長方形に対角線をひき、さらに端から5cmと8cmのところに縦の辺に平行な線を対角線までひく。そして、これらの線にそって切って、長方形をバラバラにしてから、正方形に組みなおす（図「面積が変わる図形」参照）。
両者の面積を計算してみると、長方形は5×13＝65cm²で、正方形は8×8＝64cm²で、1cm²も違っている。
種を明かすと、紙などに線を引くときに、ふつうは鉛筆の線の太さを気にしないということだ。ところが、線の太さが1mmであっても、長方形の周の長さ36cmの長さの分をずっと線の太さの内側のほうで切っていくと、あっという間に1cm²や2cm²くらい稼げてしまうのだ。このようなパズルを図形消滅パズル（increasing and decreasing areas）といい、「人間の直観があてにならないことがよくわかるから、数学による計算や証明が必要」という教育的な意味が込められている。

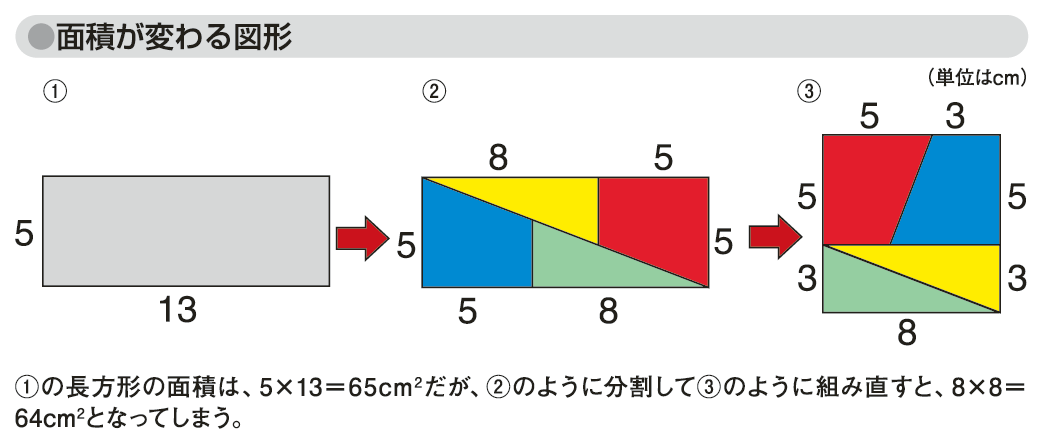
図「面積が変わる図形」