流体の不規則な流れを乱流とよぶ。飛行中にときどき出合う乱気流（turbulence）は乱流であり、鳴門海峡の渦潮も乱流化している。このように、地上のいたるところに乱流が存在するが、そればかりでなく天体にも、たとえば木星の大赤斑に見られるように乱流が存在する。円管中の流れの速度を速めると流れが突如乱流化するように、一般に流れが十分速くなると乱流になる。流体運動を支配するナヴィエ・ストークス方程式は散逸力学系の一種と見なすことができるが、乱流はこの力学系が示す決定論的不規則運動、すなわちカオスである。閉じた容器中の流体における熱対流現象（レイリー・ベナール対流　Rayleigh-B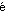nard convection）や二つの同軸円筒に挟まれた回転流体の運動（テイラー・クエット流　Taylor-Couette flow）に対しては、層流から乱流への転移がカオス力学系の立場から理論的にも実験的にも詳しく研究されている。
乱流が発達するにつれて、流速の乱れはしだいに空間的に細かくなり、そこにはある種の統計的な単純さが現れる。その代表的な性質として、コルモゴロフの相似則（Kolmogorov’s similarity law）とよばれる統計法則がある。それによれば、速度ゆらぎのパターンの統計性は、空間スケールをさまざまに変化させても、それに応じてゆらぎの振幅の尺度を適当に取り換えれば常に同一に見える。しかしながら、この法則の基礎づけや、流れのより詳細に立ち入った統計的性質の研究はまだ十分ではない。乱流の統計力学は古くから物理学における最大の難問の一つとして現代も活発な研究が継続している。