直角三角形でない三角形で、3辺の長さと面積が整数となるものをヘロンの三角形（Heron triangle）と呼び、その3辺の長さの組を「ヘロン数」という。この「ヘロン」は、3辺の長さから三角形の面積を求めるヘロンの公式（Heron's formula）のヘロンである。ヘロン数は、三角形の辺の長さが与えられて、その面積を求める入試の問題に使われる。
図「ヘロン数の例」のように、面積から有理数の高さが決まり、ヘロンの三角形は3辺の長さが有理数の直角三角形を貼り合わせたものとなる。これを5倍に拡大すると、3辺の長さが整数である二つの直角三角形を、同じ長さ（この場合16）のところで貼り合わせたものとも考えられる。
ヘロン数は無限にあるものだが、三つの辺a, b, cと面積Sの組を（a, b, c ; S）で表すと、以下のような例ができる。
（4, 13, 15 ; 24）、（3, 25, 26 ; 36）、
（9, 10, 17 ; 36）、（7, 15, 20 ; 42）、
（6, 25, 29 ; 60）、（11, 13, 20 ; 66）、…

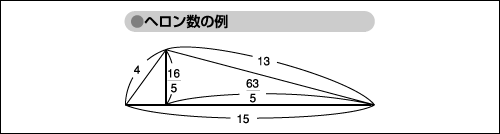
図「ヘロン数の例」