アルキメデスが円周率を3.14まで計算してから、中世の数学では、円周率の計算が数学の花形の一つであった。L.オイラーも円周率の計算に関していくつもの公式を出している。
しかし、これに関しても、関孝和とその弟子である建部賢弘が「加速計算法」によって世界に誇るべき成果をあげている。
アルキメデスや関・建部は円周率を正多角形で近似することから始めた。アルキメデスは正96角形、関は正2¹⁷角形、建部は正2¹⁰角形を用いた。
関はこの計算の中で以下の計算を実行している。2¹⁵角形の辺の長さ、2¹⁶角形の辺の長さ、2¹⁷角形の辺の長さを、それぞれ、p、q、rとして、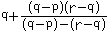

を計算すると、
π＝3.141592653589…
が算出される。これは、現在「エイトケン加速法（Aitken加速法　Aitken’s acceleration）」と呼ばれているものである。
この方法は、弟子の建部賢弘によって改良され、建部は正2¹⁰角形だけの計算から、実に小数以下41桁まで算出している。
なお、比較的簡単で精度も高い方法に、近似的な積分法である「シンプソンの公式（Simpson’s rule）」を使う方法もある。