円はすべて相似であるから、どんな円についても、（円周の長さ）/（直径）の比は一定となる。この比の値を円周率といい、π（パイ　pi）で表す。
人類が円に関する計量を始めた頃は、円周率を計測等で調べた。その値は、3とか3.16などの近似値が使われたこともある。数学史上、計算で最初に円周率を出したのはアルキメデスである。彼は、
（内接する正96角形の辺の長さの総和）＜π＜（外接する正96角形の辺の長さの総和）
から、π≒3.14まで求めた。実用的にはこれでほとんど問題がない。
これ以降、円周率が有理数かどうかを知るためにも、数学者は円周率のより精密な近似値を求めてさまざまな方法を考えていった。日本の関孝和と建部賢弘は、1722年に正1024角形の値から、収束する数列の性質を用いた効率的な「加速計算法」によって小数点以下41桁までそろばんで求めている（→「和算の円周率計算」）。
しかし、1882年にF.フォン・リンデマンがπは超越数であることを証明して、πの計算は計算機科学の領域に移っていった。この計算では、東京大学の金田康正が次々と記録を塗り替えており、小数点以下1兆桁を超えている。彼の計算によると、0～9の出現比率はそれぞれ約1/10になるというのも興味深い。

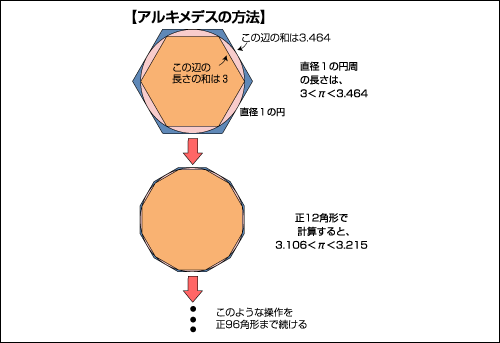
図「アルキメデスの方法」