2×2行列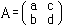

が与えられたとする。これに対し、ad－bc≠0のとき、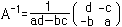

を用いると、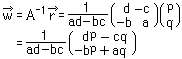

というように方程式が解けてしまう。
つまり、この場合の方程式が一意に解けるための条件が、
ad－bc≠0
であり、その解を記述するのにA^-1が有用である。
この条件式のad－bcをAの行列式と言い、detAで表す。つまり、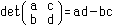

である。また、A^-1をAの逆行列（inverse matrix）という。
未知数がn個で、方程式がn個あるときは、係数を並べたものは、n×n行列となり、ベクトルはn次元ベクトルになるが、基本的な問題は変わらない。すなわち、
「A、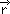が既知のとき、
A＝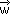
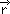
を満たす、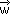を求めよ」
ということである。ただし、この場合の、行列式detAとA^-1の計算は少々複雑になるが、普通のパソコンで「Excel」等のソフトを用いることで簡単に計算することができる。
今では、行列と行列式は、変換群、可微分写像の分析など多方面に応用されている。