自然数のmを用いて、１から順にm乗したものの形の数列の和、
1^m＋2^m＋3^m＋…＋n^m＋…
を、一般にべき乗和という。特にm＝1、m＝2の場合の2式は高校の数列の和（sum of a sequence）の公式で学ぶ。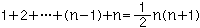


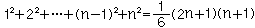
このべき乗和の公式の一般化を世界ではじめて考えたのが関孝和である。
つまり、
1^m＋2^m＋3^m＋…＋n^m＋…
のm＝11までの和の公式を手がかりに、この式のmを一般化した。その係数の表は、関の遺稿の『括要算法』（1712年）の中にある。
数年遅れて、ヨーロッパでもJ.ベルヌーイの遺稿にも記されていた。関の結果を知らなかったオイラーはベルヌーイ数（Bernoulli number）と呼び、それが定着している。しかし、独立な発見とはいえ、最初の発見者の関の名前を入れていないのは手落ちである。
なお、べき乗和の式にm=－sを入れたものがゼータ関数ζ(s)と考えられる。