関孝和が自然数のm乗の和の公式を求めようとしたのに対し、L.オイラーは自然数のs乗の逆数の無限和について調べた。つまり、次の式で表される無限の和である。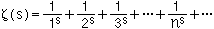

これをゼータ関数という。
とくに、s＝1のときこの式が∞になることが知られていたが、オイラーはこの分母の数を素数にしても∞になることを示した。つまり、分母が素数の単位分数の和が∞になる。整数論の権威である黒川信重によると、この事実の発見がオイラーの最も優れた業績の一つだという。

しかし、この発散の状態は非常に遅く（19桁の素数まで進んでも、4を越えない！）、直観的には、まずわからない。
さらに、このゼータ関数ζ(s)は次の式を満たすことも示した。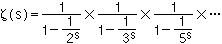

（2,3,5のところには、次々と素数が入る）
こうして、ゼータ関数が素数の分布に重要な情報を持っていることがわかり、未解決問題として名高い「ζ(s)＝0であるような複素数（→「虚数」）s＝p＋qi（p、qは実数）で0＜p＜1となるものは、すべてp＝1/2」である」という、リーマン予想（Riemann　hypothesis）につながっていく。