多角形で囲まれた立体図形を多面体という。たとえば、直方体（箱）や立方体（正6面体、サイコロ）、三角錐などがそうである。
同じ種類の正多角形で囲まれ、各頂点で同じ個数の面と辺が集まっている凸多面体をとくに正多面体という。正多面体は美しいので、数学者の興味を引いてきたが、プラトンはその形が5種類に限ることを示した。図「多面体」を参照。
正多面体の頂点、辺、面のそれぞれの数を表「正多面体の頂点、辺、面の数」にしてみると、いろいろと面白いことがわかる。
正6面体と正8面体、また正12面体と正20面体の辺の数が等しく、それらの頂点の数と面の数をお互いに入れ替えると等しい。つまり、正6面体の各面の中心に頂点を取って、それを頂点とする多面体を作ると正8面体になる。逆に、正8面体の各面の中心を頂点とすると正6面体ができる。このことを「正6面体と正8面体は双対（dual）である」という（→「双対性」）。同じことは正12面体と正20面体でも言える。

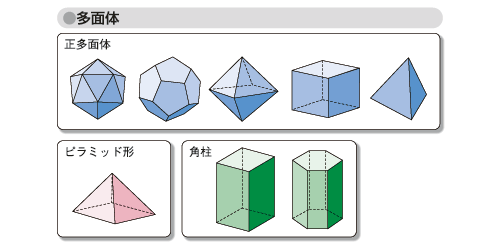
図「多面体」

表「正多面体の頂点、辺、面の数」