透視図法から生まれた射影幾何（projective geometry）では、平面に無限遠点を追加し平行線が交わる。2点A，Bに対して直線ABが決まるが、この幾何では2直線に対しても、その交点が必ず1点決まる。つまり、直線と点を入れ替えても同じ関係が成り立つ。このようなことを双対性という。
また、正6面体の各面の中心を頂点とすると正8面体になり、辺の数は一致する。逆に正8面体の面の中心を頂点とすれば正6面体が出る。同じことは正12面体と正20面体の間でも成り立つ（正4面体は自分自身）。この場合は、辺をはさんで頂点と面の関係が入れ替わる双対性の例である。
この原理はほかにも、集合論、位相幾何学など数学のさまざまな場面で双対性が見られるが、最近では物理学への応用が注目されている。

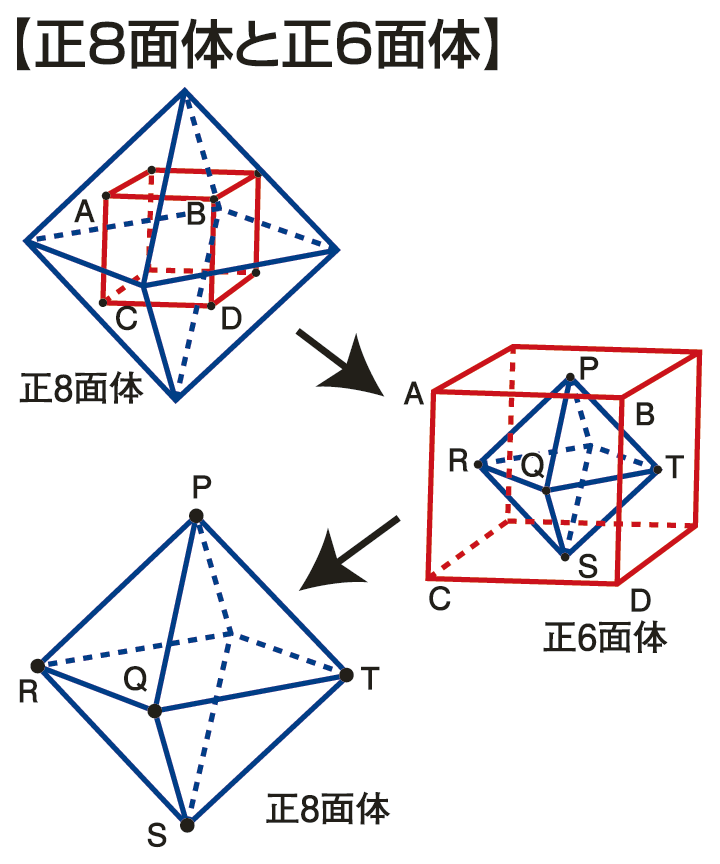
正8面体と正6面体