図「確率の難問」のように、半径が2mの大円の中に、同心円状に半径1mの小円が描かれているとする。この2個の同心円に目隠しをしてボールをぶつけるとき、大円の内側（小円の中も）に当たる確率に比べて、小円の内側に当たる確率は、どれくらいだろうか。面積の比で計算すると、大円は4m²で、小円は1m²なので、1/4と答えたくなる。
しかし、中心から放射状に、円を埋めつくすほどに無数の線を引くとすると、その線は大円については2m、小円については1mであるから、確率は1/2とも考えられる。また、この線を直線ではなく、外側へ向かうほど大きく曲がる曲線にしたとすると、この値はどのような値にもなってしまいそうである。
旧ソ連のA.N.コルモゴロフは、確率論の公理化によってこの難点を取り除き、現代の確率論が確立した。

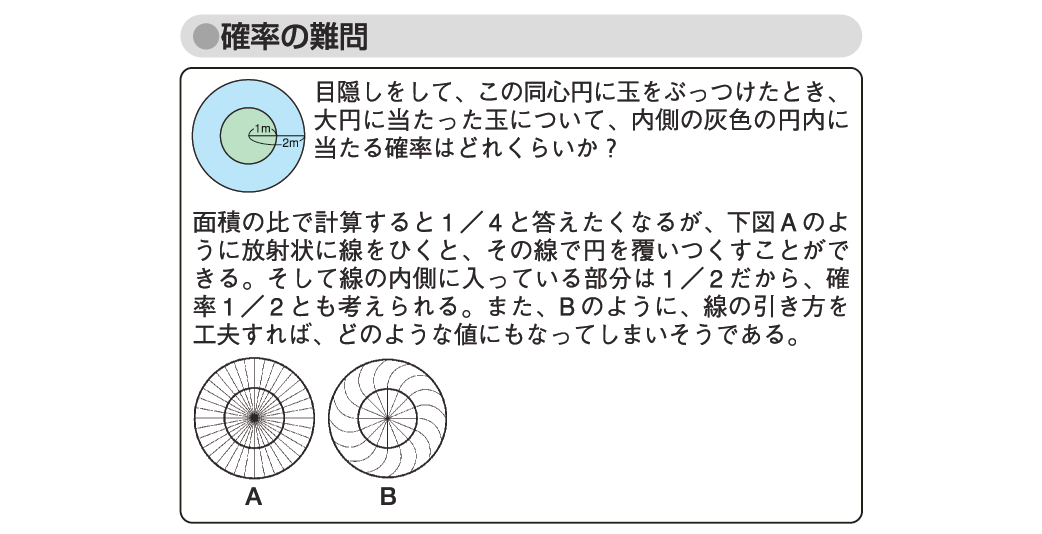
図「確率の難問」