三次元座標空間で、ある点からの距離がつねに一定の値rとなる点の全体を半径rの球面、あるいは二次元球面という（図「各次元の球面」参照）。原点を中心とする球面のうえに（x，y，z）があるならば、
x²＋y²＋z²＝r²
の式を満たすことになる。
日常で球面と言う場合は、この球面をさす。しかし、この一般化として、座標平面でx²＋y²＝r²
を満たす、点（x，y）の全体を一次元球面という。これは、円周のことである。さらに、
x²＝r²
を満たす2点をゼロ次元球面という。
一方、図で表すことはできないが、四次元座標平面の中で
x²＋y²＋z²＋w²＝r²
を満たす点（x，y，z，w）の全体を三次元球面という。
このような形で一般化すると、n＋1次元空間の中のn次元球面も定義される。
ポアンカレ予想で、最後まで残ったのは三次元球面の場合である。
一方、図「一次元球面から二次元球面を作る」のように、n次元球面からn＋1次元球面を作ることもできる。この図のように、座標平面上に円周（一次元球面）があるとき、それから二次元球面を作るには、座標平面と垂直方向に円周のコピーのつながった軸を立て（図中の1）、両端の円周をそれぞれ1点につぶして（図中の2）、なめらかにする（図中の3）、と考えられる。三次元球面も同様にして作ることができる。すなわち、二次元球面の入っている三次元空間と垂直方向に二次元球面のコピーのつながった軸を立て、その両端の球面をつぶして滑らかにすればよい。しかしながら、「三次元空間と垂直方向に軸をたてる」などという概念を思い浮かべるのは、かなり難しいだろう。

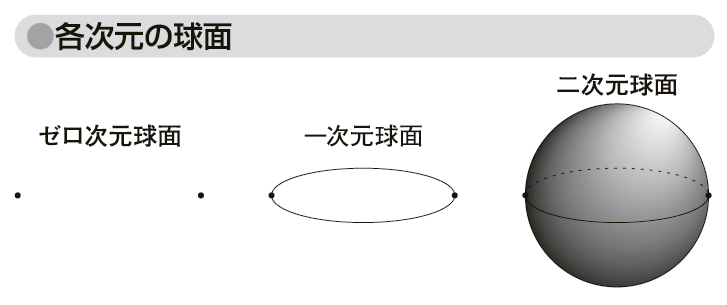
図「各次元の球面」

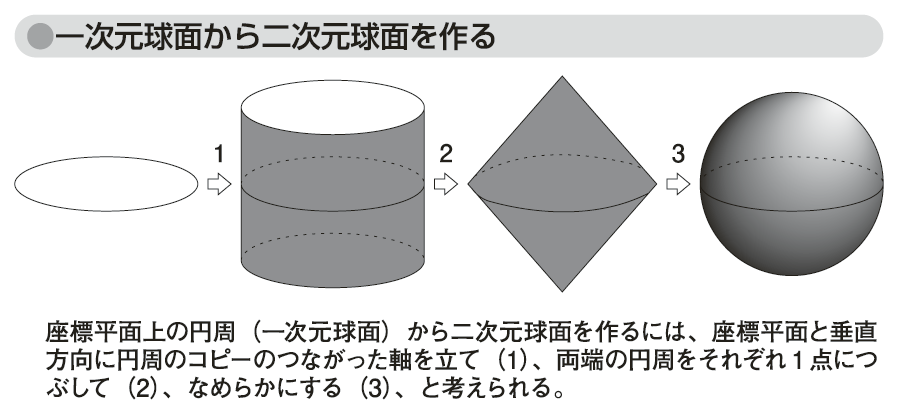
図「一次元球面から二次元球面を作る」