半径1の円を単位円という。原点が中心の単位円の周は、
x²＋y²＝1
となるが、この式は三角関数の基本的な式
sin²x＋cos²x＝1
と同じである。よって、
x＝cos t，y＝sin t
というパラメータ表示がすぐ考えられる。
図「円と三角関数」のように、単位円周上の点Pについて、OPがx軸となす角をtとしたときの座標は（cos t，sin t）となり、パラメータtが増えると、P円周上を反時計回りに回っていく。このように、数学では反時計周りの方向を回転が正の方向ということになる。また、この図から、y＝sin tのグラフは、tの増加にしたがって、波のような形になることがわかる。
この曲線は、自分で簡単に作ることができる。図「波形」のように、薄い紙を筒状に丸めて、水平線に対して45°の平面で切って開けばよい。

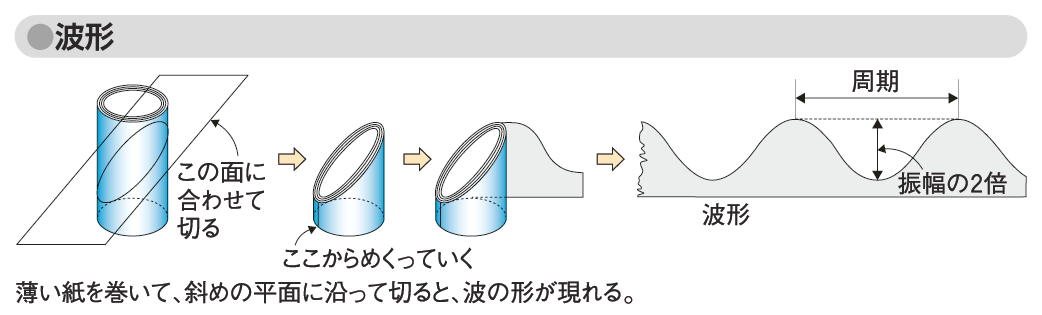
図「波形」

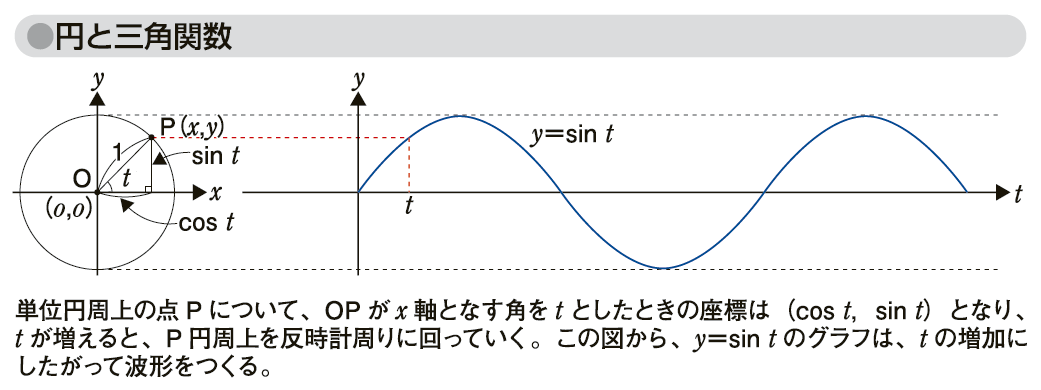
図「円と三角関数」