円筒の一方の末端を自身の内部に通して他方の末端につなげた、内部と外部の区別がつかない壺。クライン管、クラインボトルとも呼ばれる。
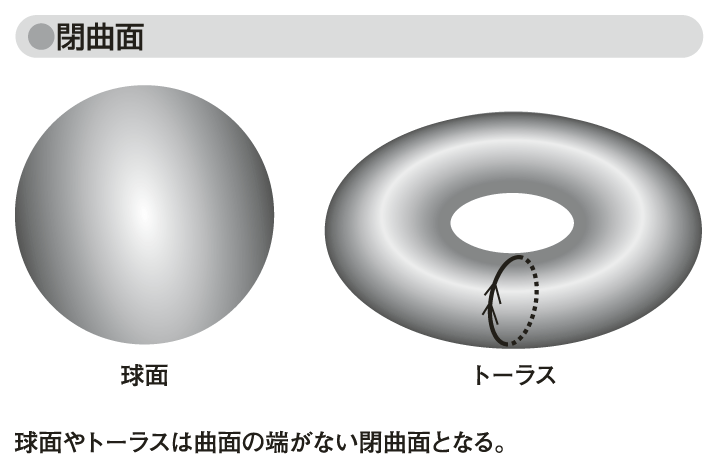
テープのような二次元状の帯をひねってつなげるメービウスの帯では、帯の面に端部という境界をもっていることになるが、球面やドーナツの表面の曲面に例えられるトーラスでは境界がない。このような曲面を閉曲面（closed surface）という（図「閉曲面」参照）。一方で、閉曲面にも裏表のないものもあり、クラインの壺はその代表例でもある。
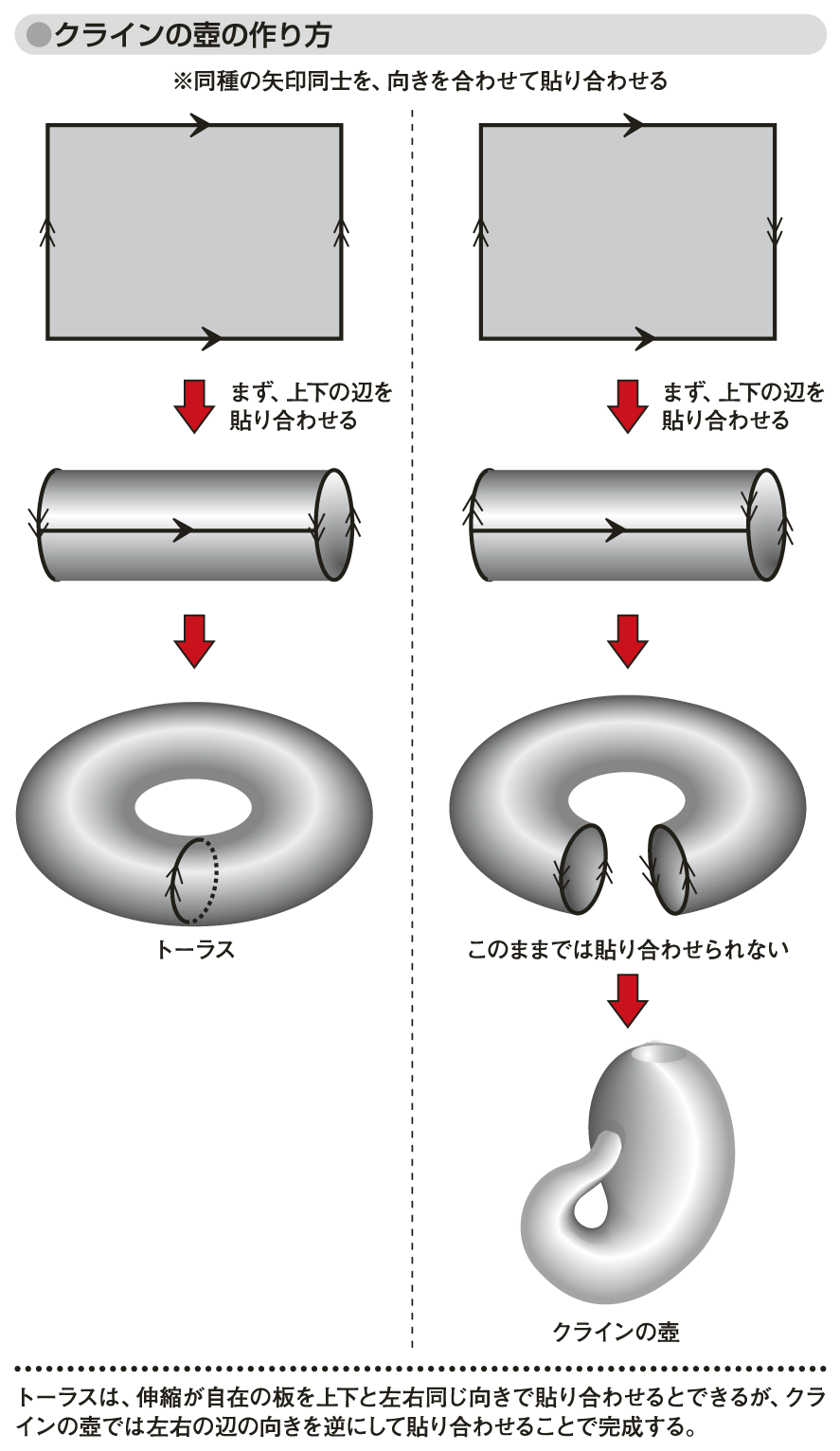
トーラスの作り方を参考にクラインの壺の作り方を述べる。トーラスは、伸縮が自在の板を上下と左右とで同じ向きに貼り合わせると作ることができる。クラインの壺はこれと同様に、上下の辺は向きを同じにして貼り合わせるのだが、左右の辺の向きは逆にして貼り合わせることで完成する（図「クラインの壺の作り方」参照）。しかし、上下の辺を貼って円筒を作り、その左右の辺からできた円を逆向きに張り合わせようとしても、簡単には貼り合わせることができない。というより、実は三次元の空間では不可能なのだ。
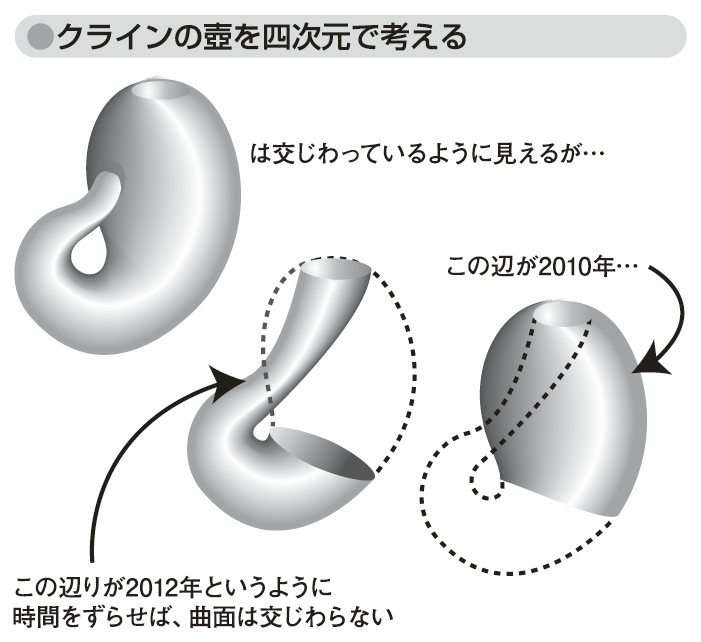
図「クラインの壺の作り方」では、曲面と曲面が交じわっているように描いてあるのだが、この図形の存在する空間を四次元にしてしまえば、実現が可能になる。三次元に時間軸を加えて四次元にしたとき、三次元では交じわっているように描かれる曲面の辺りで時間をずらすことができるようになるため、曲面と曲面を交じわらせずに、円筒の左右の円を逆向きに貼り合わせることもできるようになる（図「クラインの壺を四次元で考える」参照）。
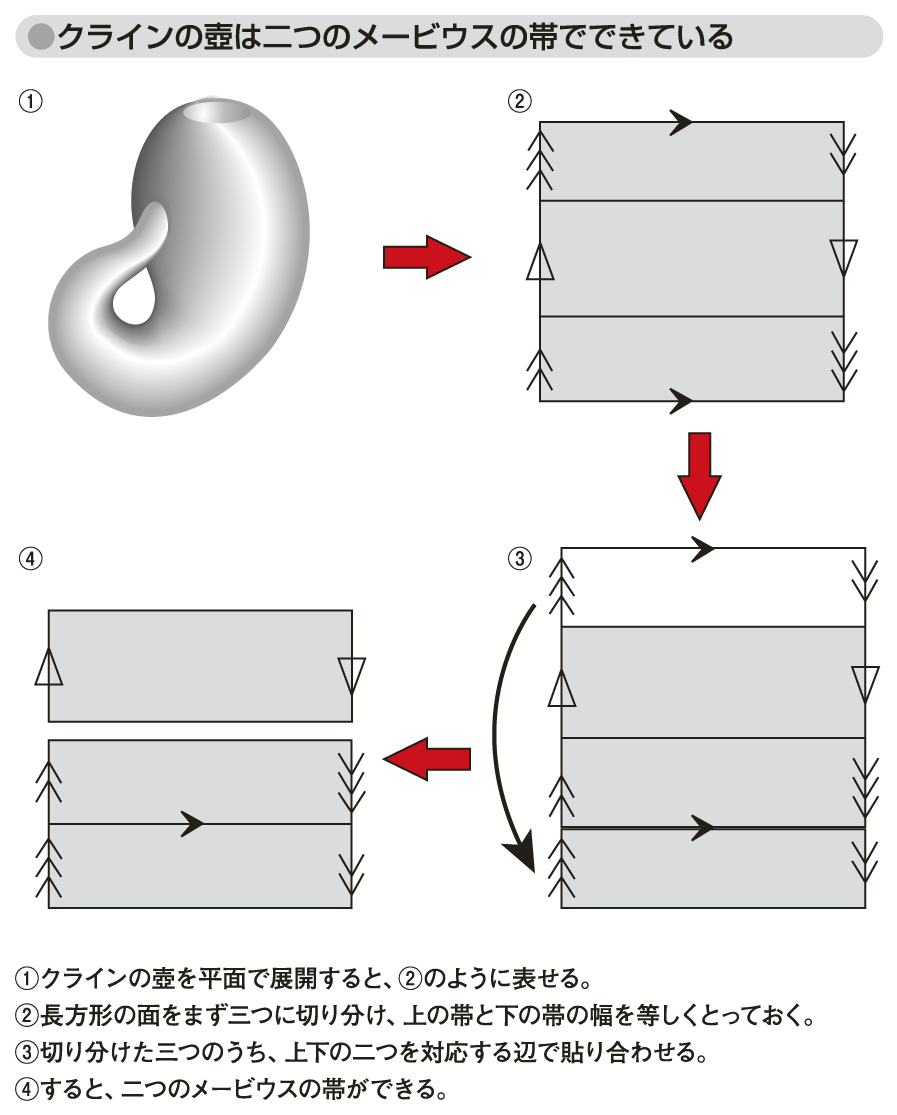
一般に、裏表のない曲面はメービウスの帯を含むことになるが、クラインの壺にも裏表がないのだから、メービウスの帯を含んでいることになる。それどころか、クラインの壺はメービウスの帯二つだけからできる曲面といえる。図「クラインの壺の作り方」をもとに考えると、まず長方形の面を三つの帯に切り分け、このとき上の帯の幅と下の帯の幅を等しくとっておく。そして、切り分けた三つの帯のうち、上下の二つを、対応する辺でつなげると、二つの帯ができる。それぞれの帯を左右の辺で逆方向に貼り合わせるとメービウスの帯が二つできることになる（図「クラインの壺は二つのメービウスの帯でできている」参照）。

図「閉曲面」

図「クラインの壺の作り方」

図「クラインの壺を四次元で考える」

図「クラインの壺は二つのメービウスの帯でできている」