図「確率のパラドックス」の一番上にあるような2個の同心円があり、外側の円の半径が2mで内側の半径は1mとする。目隠しをして、この同心円に玉をぶつけたとき、外側の大円の部分に玉が当たる確率に比べて、内側の小円の内側に玉が当たる確率はどれくらいになるか。面積の比で計算すると、大円は4πm²で、小円はπm²なので、4分の1と答えたくなる。
しかし、図のAのように放射状にたくさんの直線を引くと、小円の内側に入っている部分は2分の1だから、小円に玉が当たる確率は2分の1とも考えられる。しかし、この理屈も、Bのように小さい円の内側は直線でありながら、外側では大きく曲がるように線を引くよう工夫すると、どんな値にでもなってしまいそうに思える。ソ連のA.N.コルモゴロフは確率論の公理化によってこの難点を取り除き、現代の確率論が確立した。

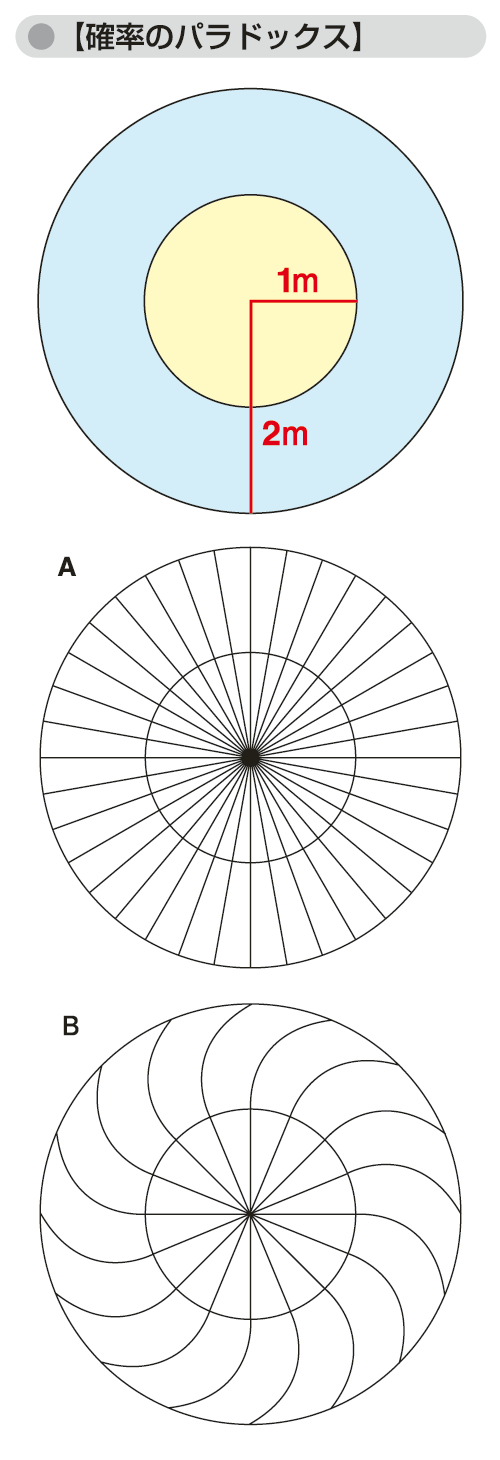
確率のパラドックス