自然数だけを並べた自然数列（progression of natural numbers）から合成数（約数をもつ自然数）をふるい落として素数（1と自身以外に約数をもたない2以上の自然数）だけを残す手順のことで、紀元前200年ごろに活躍したエラトステネスが考案した。一般には、10列に並べることが多いが、自然数を1から順に6列に並べるほうが操作が簡単である。つまり、図「エラトステネスの篩」のように1行目は1～6、2行目は7～12、3行目は13～18、……と数字を列記していく。そして、まず1だけは除外する。次に小さな数2は素数となる。その2を残し、2の倍数（2、4、6列目のすべて）を消す。残った中で最も小さな数3は素数。その3を残し、3の倍数（3、6列目のすべて）を消す。残った数の中で最も小さい5は素数だから、5を残し、5の倍数を消す。
こうして、17の素数まで進むめたものがこの図であり、100までの素数がすべて篩に残っている。この図から、2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97が100までの素数である（実は、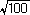＝10より下の7までの素数で篩にかければよい）。
また、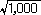＝31.62の直前の素数まで、つまり31までこの操作を続けて残ったものが1,000までの素数となる。
前記の2～101の素数の例でみると、2，3，5，7のあたりは密集しているが、だんだんまばらになっていく。100までの中では、89と97の差が9で最も広い。このまま間隔がどんどん広がるのかと思うと、101と103の間は2である。10,000までのスケールでは、34の差があるところが2カ所ある。数をどんどん広げると、いくらでも間隔の広いところを見つけることができる。
このように素数の分布は不規則だが、大きなスケールでは、規則性が見えてくる。π(x)をx以下の素数の個数とするとき、xを大きくすると、π(x)は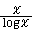に限りなく近づく。このように解析による整数論研究の方法を解析数論（analytic number theory）という。

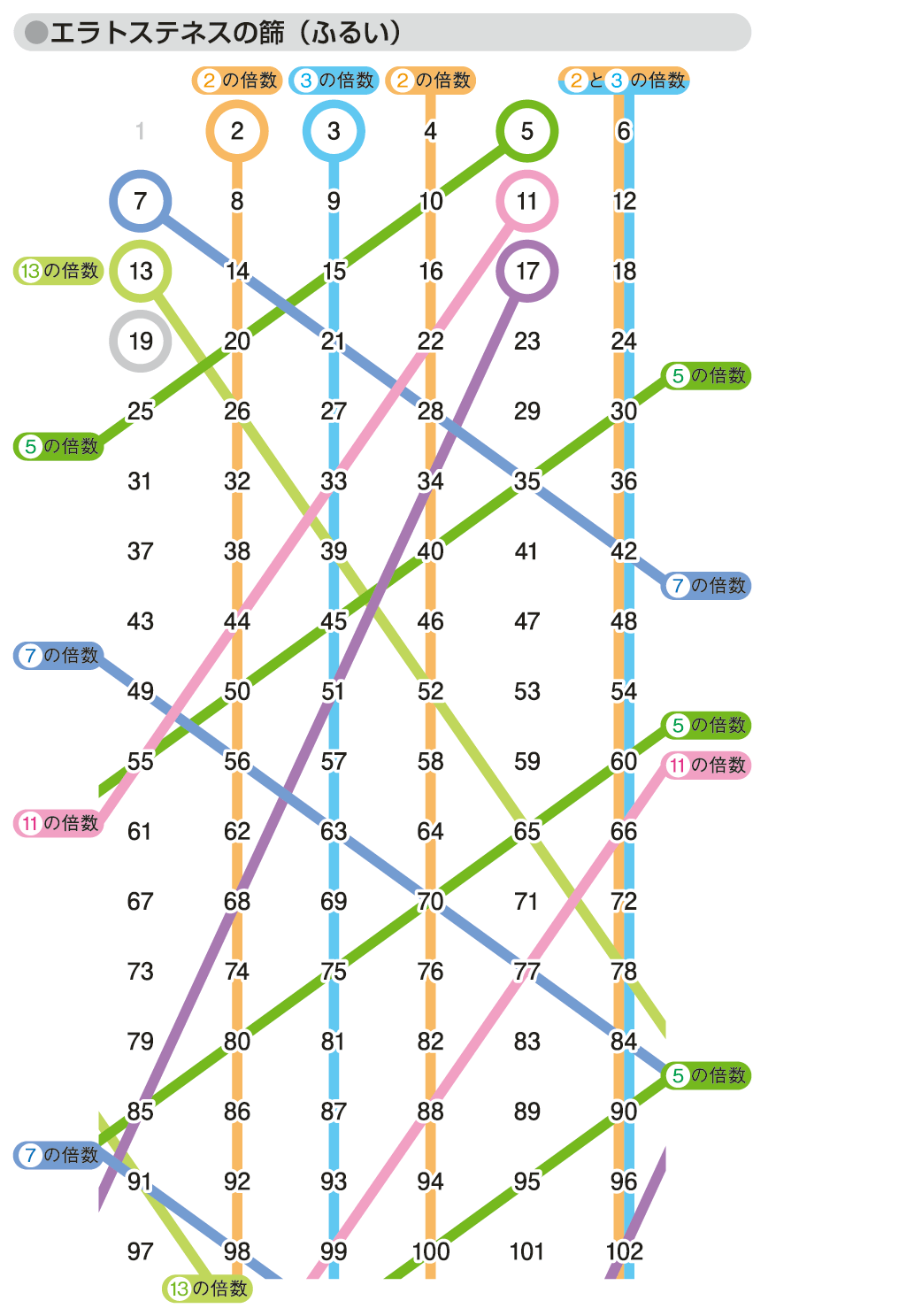
エラトステネスの篩（ふるい）