2以上の自然数pが1とpの他に約数をもたないとき、それを素数といい、それ以外を合成数という。素数は2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ……など無限にあるが、一方で「自然数の原子」のような単位と考えられている。それは素因数分解定理によって、自然数はつねに一通りの形で素数の積に表されるからである。たとえば、169と168はわずか1しか違わないが、素因数分解をすると、13²と2³×3×7で、かなり違う数とも考えられる。
2～31までの例では素数の分布は不規則に見えるが、大きなスケールで見ると規則性が見えてくる。π(x)をx以下の素数の個数とするとき、xを大きくすると、π(x)は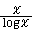に限りなく近づく（→「素数分布」）。このように、解析を用いて整数論を展開する方法を解析数論（analytic number theory）という。
今や素数の理論はコンピューターの公開鍵暗号システムに最も有用なものであり、大きな桁の素数を作ることが大変重要な意味をもっている。一定の手順によってできる素数にはメルセンヌ素数とフェルマー素数がある。