カオス現象に関する理論は、せいぜい数個の力学的自由度（dynamical degrees of freedom）を含むシステム、すなわち低次元力学系（low-dimensional dynamical system）に見られる不規則現象が主な対象になっている。このようなカオス現象を特に低次元カオス（low-dimensional chaos）と呼ぶ。これに対して、同じく決定論的な運動法則に従いつつ、非常に大きな自由度をもつシステム、すなわち高次元力学系（high-dimensional dynamical system）に見られる不規則な振る舞いも自然界に普遍的に存在し、これは高次元カオス（high-dimensional chaos）と呼ばれる。システムが空間的な広がりをもつ場合の高次元カオスは、時間的な不規則性に加えて空間的にも乱れた構造を示すことから時空カオスと呼ばれる。たとえば、閉じた容器中の流体における熱対流現象であるレイリー・ベナール対流（Rayleigh-B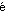nard convection）がレイリー数（Rayleigh number　レイノルズ数に相当する無次元量）の増大とともに乱流化する場合を考えると、発生直後の乱流状態は低次元カオスで記述できるが、次々に流れの不安定が起こるにつれて高次元カオスに移行する。十分に発達した乱流は時空カオスの典型例である。時空カオスは流体現象以外にもさまざまな形で存在する。たとえば、2007年のノーベル化学賞受賞者であるG.エルトゥルの研究グループでは、白金表面における一酸化炭素の酸化反応において、反応と拡散の効果および気圧変化を通しての大域的な相互作用の効果のからみあいから時空カオスが起こることが実験的に確かめられた。成長しつつある界面（interface）においても、しばしば時空カオスが見られる。たとえば、燃焼（combustion）の過程における炎の前面はしばしば複雑な形状が不規則に時間発展する時空カオスとなる。