ヨーロッパで日本での「ねずみ算」に対応するのが「うさぎ算（Fibonacci rabbit sequence）」である。L.フィボナッチの『算盤の書』には「最初生まれたばかりのうさぎの1つがいがいる。このうさぎは1カ月たつと成熟し、2カ月目から毎月1つがいの子を産むとする。このとき、1年間につがいの数はどのようになるだろうか？」とあり、この状況を示したのが、図「うさぎ算」である。つがいの数は、
1, 1, 2, 3, 5, 8, 13,…
と増えていくことがわかる。1＋1＝2、1＋2＝3、2＋3＝5、3＋5＝8というように、この数列のどの項も、二つ前の項と一つ前の項を足したものになっていることに気付くだろう。この法則で8項目から先に続けると、
21, 34, 55, 89, 144, 233となる。1年後は、12カ月後だから13項目の233つがいが求めるものとなる。
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
と並んでいる数の列を紹介者にちなんでフィボナッチ数列という。
この数列のn番目の項とn－1番目の項の比を順に取ると、
1/1＝1、2/1＝2、3/2=1.5、5/3=1.667、8/5=1.6、13/8＝1.625、21/13＝1.61538、34/21＝1.61904、55/34＝1.61764、89/55＝1.61818、144/89＝1.61797、233/144＝1.61805、…となる。この値は小数第6位以下を切り捨てているが、1.618のあたりに近づいていくことがわかる。実際には黄金比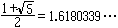

に近づくのである。
また、フィボナッチ数列は松かさやひまわりの種の配列をはじめとして、自然界のさまざまなところに見られるという。

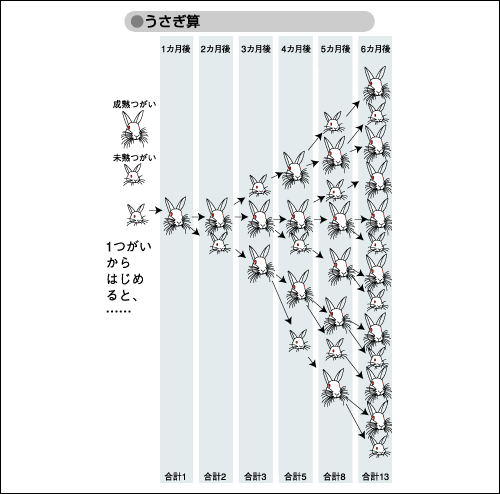
図「うさぎ算」

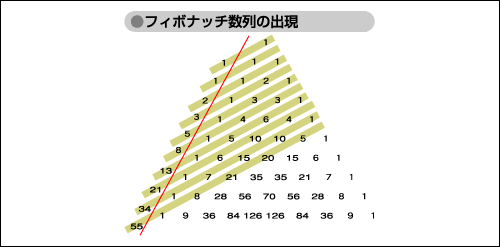
図「フィボナッチ数列の出現」