図「パスカルの三角形」の端に1を配置し、各点で上から矢印に従って入ってくる数字の和を書くことにすると、右側の図のパスカルの三角形になる。
この図の、n＋1段目の数字は、(x＋1)ⁿを展開して「降べき」に整理したときの係数の表になっている。たとえば、(x＋1)⁸の係数は実際に計算しなくとも、この表の9列目を見れば、以下のようになることがわかる。
(x＋1)⁸＝x⁸＋8x⁷＋28x⁶＋56x⁵＋70x⁴＋56x³＋28x²＋8x＋1
この表は11世紀中頃の中国で文献に現れたという。しかし、名前はこの表の応用をたくさん示したB.パスカルにちなむ。
この表の中にフィボナッチ数列が隠されているのは大変おもしろい。実際、図「フィボナッチ数列の出現」のように斜めに加えていくと、1, 1, 2, 3, 5, 8, 13, 21, …とフィボナッチ数列が現れてくる。
また、三角数もこの中に見ることができる。図「パスカルの三角形」の1が並ぶ左斜辺から3番目の並びを見ると、ここに1，3，6，10，15，21，28，36と、三角数が出てくる。原理から考えると、上からn＋1番目の行が(x＋1)ⁿの展開式の係数だから、3番目には、
_nC₂＝n(n＋1)/2が並ぶのである。

図「パスカルの三角形」

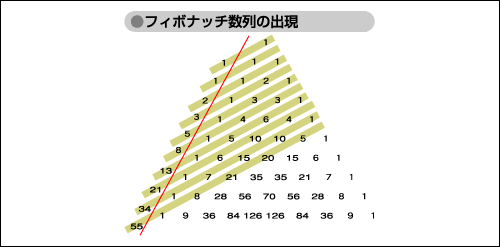
図「フィボナッチ数列の出現」