整数論を研究していたG.H.ハーディは、「役に立つ数学は邪道であり、役に立たない数学こそ尊いのだ」と主張した。
だが、皮肉なことに、素数・合成数（1と自身以外に約数をもたない2以上の自然数が素数、それ以外が合成数）の判別とその分解は、最も応用の大きい分野の一つになった。
コンピューターが発達し、通信と結びついたので、情報が漏れると多大な損害に結びつく。それを防ぐために情報の暗号化（encryption）が必要になった。
その方法として、1970年代後半から公開鍵と呼ばれるRSA法（R.L.リヴェスト、A.シャミル、L.M.アドレマンの頭文字）が用いられている。そのやり方は次の通り。
まず、すべての文字を数字で表す。通信の受け手のAさんは鍵である二つの数字MとL（たとえば、L＝51、M＝3とする。未公開鍵は11）を公開する。通信の送り手Bさんは、たとえば、7を送るには、7をM乗してLで割った余りを送ればよい（この場合、7³＝343を51で割った余り37を送る。Aさんは、隠していた鍵N（＝11）を使って、37¹¹を51で割って余りを出すと、その7になる）。
この方法は、次のような整数の性質を用いて実現されている。
「pとqは異なる素数であるとする。このとき、MNを(p－1)(q－1)で割った余りが1ならば、(X^M)^Nをpqで割った余りはXである」
Bさんがある数XをM乗してLで割った数をAさんに送る。Aさんはその数をさらにN乗して、Lで割って余りを計算すれば、Xを得る。この場合、X^MをLで割った余りを出すことを、Xの公開鍵による暗号化、(X^M)^NをLで割って、最初のXを出すことを秘密鍵による復号という。
この暗号を解読しようとしている人が、“Bさんが37を送った”ことを知っても、もう一つの鍵11を手に入れないと、そこから37¹¹を51で割った余りの7が出せない。
盗聴者は、公開されている数L（この場合51）についてL＝pqの形にすればMからNが出る。しかし、Lを大きくすれば、p、qを出すことは極めて困難になり、これがこの暗号化の安全性のよりどころ。
当初p、qそれぞれ100桁位で安全だったが、計算機の高性能化で、さらに大きな桁が使われている。
このことからも、桁数の大きい素数を作り出すことが大変実用的な価値を持つこととなったのである。
なお、2009年に放送された『NHKスペシャル ～リーマン予想・天才たちの闘い～』によって、素数の分布がわかれば公開鍵暗号が無力化すると受け取った人たちがいるらしいが、素数分布がわかっても、暗号は大丈夫である。素数分布によって素数がすべて出てくるわけではなく、仮に出てきたとしても、例えば、100万桁の素数の数は、π(10^1,000,000)となり、10^1,000,000/log 10^1,000,000ほどあって、全部試すことなどまずできないだろう。

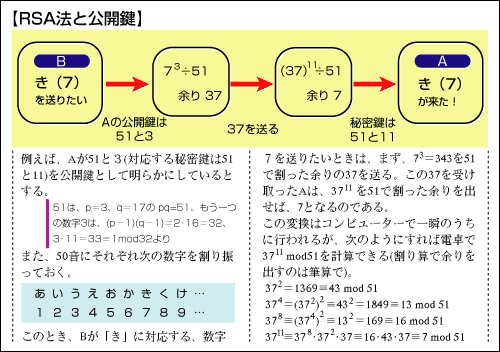
図「RSA法と公開鍵」