自然数nについて、π(x)をx以下の素数（1と自身以外に約数をもたない2以上の数）の個数と定義する。この関数がどういうものであるかを決定すると、素数の分布が明確になる。2，3，5，7，11，13，17，19，23，29，31，……と、素数を並べると、分布が不規則に見える。しかし、大きなスケールでは、規則性がある。これを見るために、π(x)をx以下の素数の個数とする関数として、π(x)を調べると、図「素数の分布」のような階段状のグラフになる（図はx≦100の範囲）。
これくらいの段階では、グラフは階段状で、連続的な関数に近似することは考えられない。しかし、ガウスは15歳のとき、xを大きくすると、π(x)が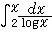

に限りなく近づくことを発見した（この対数の底はe）。この近似式は100年たって、証明された。なお、この関数は、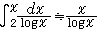

と近似されるので、粗い言い方では、「π(x)は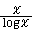に近づく」と言うことがある。このように解析による整数論研究の方法を解析数論（analytic number theory）といい、素数分布の解明の問題がリーマン予想へとつながっていく。

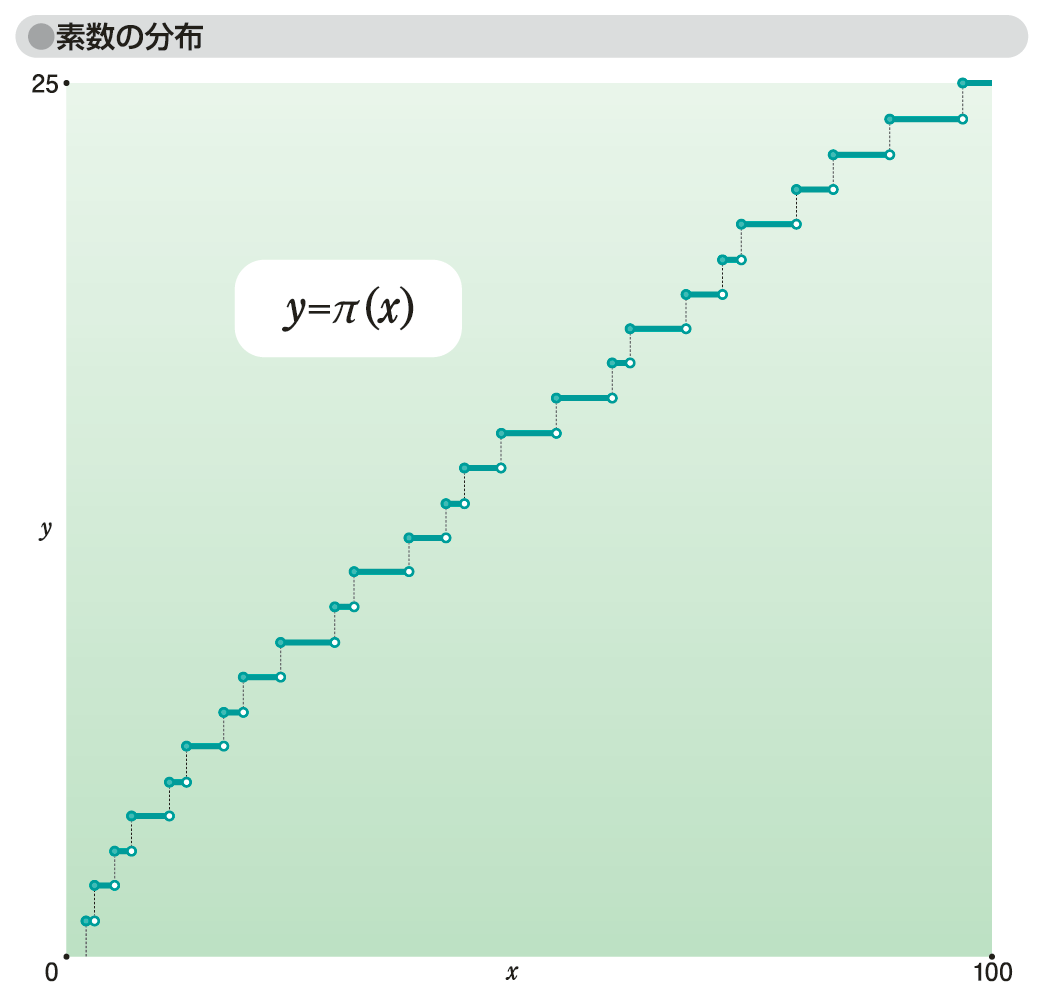
素数の分布