関数は、性質のよくわかっている多項式で近似することによって分析しやすくなる。多項式への近似がテイラー展開である。
そもそも、関数y＝f(x)のx=aでの微分係数f’(a)は、y＝f(x)のグラフのx＝aでの接線の傾きで、意味するところは、
f(x)≒f’(a)(x－a)＋f(a)
と考えられる。つまり、（a, f(a)）に近いところでの、y＝f(x)の一次関数への近似式のxの係数が微分係数である。この近似式でも関数の増減、極値など多くの情報が得られる。
凹凸などの情報になると、二次関数への近似が必要となる。さて、y＝f(x)を二次式で近似したとして、(x－a)²，(x－a)で展開して、
(x－a)²， (x－a)の係数を考えてみよう。
f(x)≒p(x－a)²＋q(x－a)＋r
とおいて、微分を繰り返してみると、
f’(x)＝2p(x－a)＋q , f”(x)＝2p
これら式のxにaを代入すると、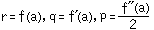

つまり、x＝aのまわりで

となる。この操作を続けていくと、f(x)は、x＝aのまわりで、次式に近似される。