ユークリッドは『原論』13巻に古代エジプトの数学をまとめ、以後の文化の方向に大きな影響を与えた。その特徴は演繹（えんえき）的な証明の積み重ねである。そのために、定義、論理の進め方の公理（axion）、前提になる五つの命題の公準（postulate　現在ではこちらを公理という）を仮定している。
『原論』の弱点は、冗長な第五公準「ある直線lの外の点Pに対し、Pを通りlと交わらない直線が一本だけ引ける」で、これを他の公準から導こうとした試みはすべて失敗した。逆に、19世紀初頭にハンガリーのJ.ボーヤイらは、他の公準はそのままで、Pを通りlに交わらない多数の直線が引ける幾何学を作った。その後、ドイツのB.リーマンは平行線がない幾何学を作った。
この二つの幾何学を「非ユークリッド幾何学」、旧来の幾何学を「ユークリッド幾何学」という。この幾何学の登場は、形式主義を生み、公理の独立性や無矛盾性を議論する基礎論の成立を促した。

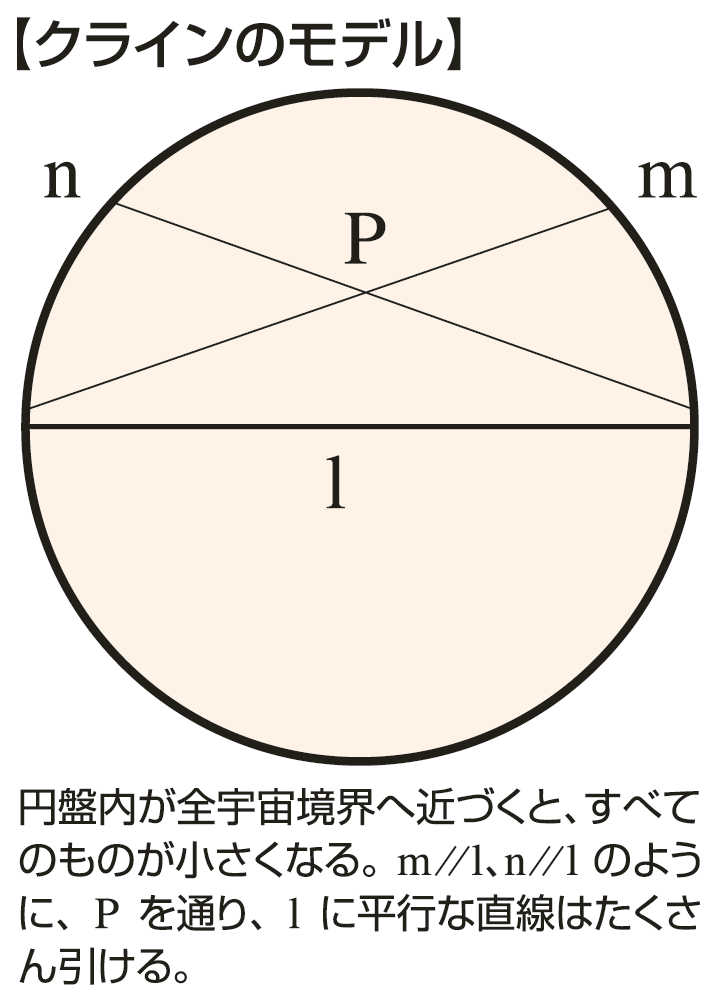
クラインのモデル