数の中には有理数の他にも、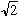や、x³＝2をみたす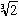、x^r＝mをみたす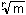などの無理数があることがわかった。
では、実数は、有理数と、ここにあげたような無理数を有理数倍したものの四則演算や累乗根で出てくる数だけなのだろうか。実は、今まであげた数はすべて整数係数の多項式による方程式の解になっている。たとえ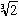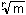ば、－は、
x⁶－9x⁴－4x³＋27x²－36x－23＝0
の解である。このような数を代数的数（algebraic number）という。
19世紀の終わり頃から、代数的数でない数も存在することがわかってきた。これが超越数である。よく知られた数では、円周率πと自然対数の底eや、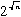とか、log_en（いずれもnは自然数）などがある。見るからに超越数のe＋π、e×πがいまだ不明なのもおもしろい。
全体集合とその部分集合などを表すヴェン図式（Venn diagram）では、超越数と代数的数、有理数と無理数が対等に書いてあることが多いが、実際には、実数の中のほとんどは無理数で、無理数のほとんどが超越数である。つまり、実数を定義することが難しいのは超越数に起因する。