紀元前2000年ごろのバビロニアで発見されていた直角三角形の3辺の関係式をピタゴラス学派が定式化した。そうすると、彼ら自身が矛盾に苦しむことになった。ピタゴラスの定理は、直角三角形の3辺の長さをa，b，cとすると、
a²＝b²＋c²を満たすというもの。ここで、これを二等辺三角形にして、a＝b＝1とすると、たちまち、有理数の世界では身動きできなくなる。cは、
c²＝1＋1＝2
を満たさなければならなくなり、整数の比に表せない無理数になるのである。このことは、後のユークリッドによって明示された。
なお、図のように三角形の各辺の長さをもつ正方形を考え、そのうちの小さいほう二つを切って、大きい正方形に並べる「証明」がいくつかある。しかし、本当の証明と呼ぶには、切ってできた多角形と対応する多角形（たとえば、Bの(3)とCの(3)）が本当に同じものであることを示さなければならない。このときに、(3)の四辺形を二つの三角形に切って、三角形の合同条件を用いて証明することになる。正方形を切って並び替える方法のうち、ここにあげた方法は平行移動だけでできることもあり、もっとも証明が楽になる。

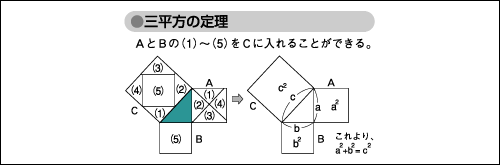
図「三平方の定理」