二つ以上の図形が、その形と大きさにおいて完全に同一であること。二つの三角形が相似で、相似比が1：1であれば合同である。二つの三角形が合同であるための条件を合同条件（congruence condition）という。合同条件では、「相似比が1」であることを示すために、辺の長さを条件に含める必要がある。
△ABCと△DEFについて、以下のいずれかが成り立てば、△ABC≡△DEF（「≡」は合同を表す記号）である。
(1)3辺の長さが等しい。
(2)2辺とその2辺にはさまれる角が等しい。
(3)二つの角とその間の辺が等しい。
有名なピタゴラスの定理（三平方の定理）の証明にも三角形の合同条件が使われる。この合同条件によって、三角形では、3辺の長さが決まれば、図形は1個だけ決まる。ところが、四角形では、そうはいかない。建物を補強する筋交いも、このままだと動きやすい長方形の枠組みを、三角形に分割して動きようのない形にしたものである。

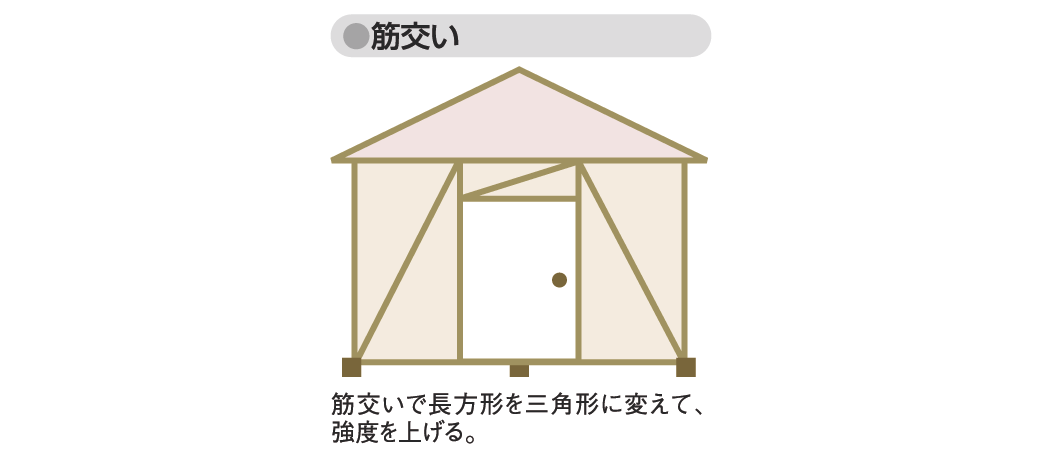
図「筋交い」