6は、自分自身と友愛数である。たとえば、6の約数をあげていくと、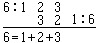

自分自身と友愛数になる数のことを完全数という。言い換えると、ある数（この場合6）の約数のうちで、その数自身を除いたもの（この場合、6を入れないので、1, 2, 3）の和（1＋2＋3）がその数（6）になるとき、完全数である。
メルセンヌ素数2^q－1を見つければ、（2^q－1）2^q-1が完全数となることはユークリッドが示している。なぜなら、その約数は、
1, 2, 2², …, 2^q-1, (2^q－1), (2^q－1)2, (2^q－1)2², …, (2^q－1)2^q-2
となるが、それらを加えると、
(1＋2＋2²＋…＋2^q-2)｛1＋(2^q－1)｝＋2^q-1＝(2^q－1)2^q-1
となるからである。
古代ギリシャ時代には、28＝(2³－1)2²、496＝(2⁵－1)2⁴、8128＝(2⁷－1)2⁶の四つが完全数として知られていた。qに7の次の素数の11を入れると、(2¹¹－1)＝2047＝23×89で、メルセンヌ素数ではなく、(2¹¹－1)2¹⁰は完全数ではない。
メルセンヌ素数から作る完全数は偶数となるが、奇数の完全数があってもよいはずである。しかし、奇数の完全数はまだ発見されていない。