自然科学、工学、経済学などのいろいろな状態は、微分方程式の解として記述される。ところが、実際はそこにランダムな影響が加わる場面が多い。最も典型的なランダム量はブラウン運動（Brownian motion）と呼ばれ、確率論の主要な研究対象である。このような状態を記述するために、伊藤清はランダム量を含む微分方程式を確率微分方程式として導入した。M.ショールズらは、この理論でブラック・ショールズ方程式（Black-Sholes equation）を作り、デリバティブ取引に用いて一時期大成功を収めた（ただし、ロシア金融危機では失敗）。彼らは、これでノーベル経済学賞を受賞した。
伊藤自身も1998年に京都賞を、2006年にガウス賞を受賞した。
ある期日にある価格で原資産（株やもの）を買う「権利」をコール・オプション（call option）という。これは、その期日に価格が満足できなければ放棄することができる。ただし、オプションの購入代金は損をする。
これに対してのプレミアムPの計算式は以下の通り。

ただし、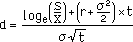

S：原資産の現在の市場価格
X：権利行使価格
t：満期までの年数
r：短期金利（安全利子率）
σ：原資産の価格変動率、年率でN(d)＝1－I(d)（標準正規分布→「正規分布」）