正多面体について、正4面体、正6面体、正8面体、正12面体、正20面体のそれぞれの頂点の数、辺の数、面の数を比べると、次の関係があることがわかる。
頂点の数－辺の数＋面の数＝2
この「頂点の数－辺の数＋面の数」をオイラー標数という。
この名前は、「オイラー標数が2になるのは、多面体の位相幾何学の性質によるものである」とL.オイラーが示したからである。
つまり、多面体を伸縮性のあるゴムでできていると考え、それを伸び縮みさせて分類すると、正多面体はすべて球面になる。伸び縮みさせて球面になることが、オイラー標数＝2であるための条件である。図「オイラー標数が2のときの正多面体」のように、角柱やピラミッド形なども球面になり、オイラー標数＝2である。
一方、図「オイラー標数が0のときの多面体」のような多面体を膨らますと浮き輪になり、これのオイラー標数は0となる。
この曲面はトーラス（Torus）とも呼ばれる。さらに、膨らますと2人乗り浮き輪になる多面体や、3人乗り浮き輪になるものもあり、一般にn人乗り浮き輪のオイラー標数は－2(n－1)になることがわかる。
こうして、一般に曲面（二次元）と呼ばれているもののうち、ふちのないものは、オイラー標数で完全に分類されるのである。
オイラー標数は、位相幾何学の性質（伸び縮みをしても同じ）を代数的な量で分類した最初のものである。

表「正多面体の頂点、辺、面の数」

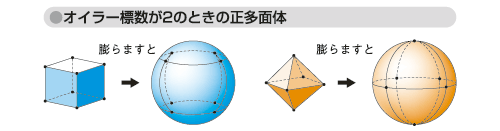
図「オイラー標数が2のときの正多面体」

図「オイラー標数が0のときの多面体」