直角三角形では、直角以外の角を決めれば、もう一つの角も決まる。また、ピタゴラスの定理によって二つの辺の長さからもう一つの辺の長さが決まる。建築現場では、水平に対してAの角度の建築物を作るとき、それは「Aの傾き」というかわりに、「水平距離がbのとき、高さaになる角度」と表現したほうが実際的となる。このように、角度を直角三角形の相似比を用いて表現する方法を三角比という。
ある任意の直角三角形について、図のような鋭角の角度をAとし、垂直な辺をa、底辺をb、斜線をrとするとき、∠Aを中心に考えると、代表的な三角比の表現は次の三つとなる。
a/rをAの正弦、sinA（サインA）
b/rをAの余弦、cosA（コサインA）
a/bをAの正接、tanA（タンジェントA）
これらの比の値は、いずれも∠Aの大きさによって決まる。これらをまとめて、∠Aの三角比という。このAを変数として、角度Aを＋－両方向に拡張し、その値を関数と考えると、一定の周期で波形を繰り返す周期関数である三角関数が出てくる。

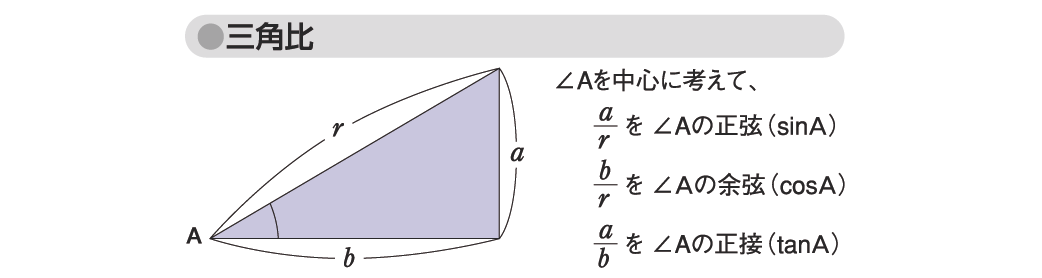
図「三角比」