微分方程式は、何回か積分して解くのが普通である。しかし、三体問題の場合のように、積分ができないこともある。フランスのH.ポアンカレは微分方程式を幾何学的に捉え直した。つまり、微分方程式は空間の各点に連続的にベクトルを与えた状態と考える。これをベクトル場（vector field）といい、微分方程式を解くことは、これらのベクトルを接線にもつ解曲線（solution curve）を描くことである。これは各点での方向と速度を与えると、目的地に着く自動航行装置と同じ。
解曲線を集めて曲面にしたのが解曲面（solution surface）である。ポアンカレは解曲面の分類により大きな成果を上げた。これが曲面の分類へと進み、位相幾何学に発展する。また、ベクトル場と解曲線、解曲面の関係を扱うのが力学系である。点xが一定の時間後に解曲線に沿って移った先をf(x)として関数を定めると、力学系はf(x)の状態を研究する分野とも考えられる。

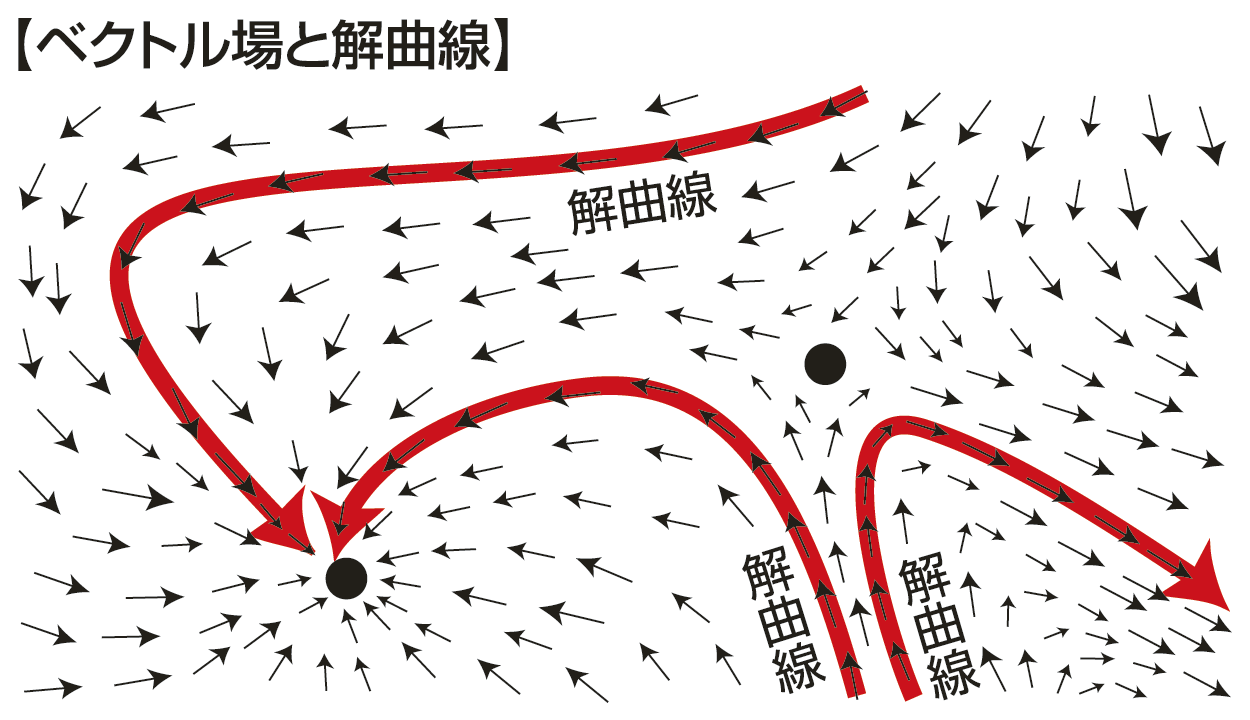
ベクトル場と解曲線