テイラー展開の式にa＝0を代入したとき、マクローリン展開という。
特に、自然対数の底eと三角関数に関する次の三つがよく使われる。



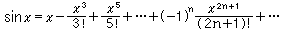
L.オイラーは、この一番上の式のe^xに虚数iを用いたx＝ixを代入して、実数部分と虚数部分に分けて計算した。

すると、以下の式になる。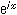
＝cos x＋i sin x
こうしてオイラーは、自然対数の底eと虚数iと三角関数を結びつけたのである。とくに円周率πを用いた、x＝πのとき、この式は、
＝－1
となる。
eとiとπという、とてつもない組み合わせで、最終的に－1という整数値になるという、まったくもって意外な結果である。
この公式ほど数学の意外性の美を感じさせるものはないだろう。実際、数年前にアメリカのある団体が数学関係者を対象にした「定理あるいは公式で一番素晴らしいものをあげよ」というアンケートで、このオイラーの公式がトップになったという。また、小川洋子の小説『博士の愛した数式』でも、この数式が重要なキーワードになっている。