三次元の中で、二つ以上の円、または円と同相（伸び縮みにより重ね合わせられる図形→「トポロジー」）な図形が入っている状態をいう。すべての円がお互いから分離できる状態を「自明な絡み目（trivial link）」といい、分離できない状態を「自明でない絡み目（non-trivial link）」という（図「自明でない絡み目」参照）。三つのループの図形である三輪違いの紋（ボロミアンリング）なども「自明でない絡み目」の一つである。
絡み目が自明でなく、二つの輪が絡んでいてお互いから分離できないことを示すには、球体の材料からこの形になるようにくりぬいたものと、球体の材料から二つの絡んでいない輪をくりぬいたものが同相でないことを示せばよい。しかし、証明はそれほど簡単ではない。例えば、一次元の場合と二次元の場合とで、二つの輪が「自明でない絡み目」を作っているとする。このとき両者とも、輪が外れないことは容易にわかる（図「一次元と二次元では絡み目は外れない」参照）。しかし、次元が高くなって三次元になり、さらにこれがやわらかい粘土でできていると、次元が高くなることにともなう自由度のため、直観的にはあり得ないことが起こり、絡み目を外すことができる（図「三次元では絡み目を外せる」参照）。
「単連結な三次元多様体は球面と同相か」という問題を提起したポアンカレ予想では、五次元以上の場合については早くから解決していたにもかかわらず、次元を低くした四次元や三次元ではなかなか解決できなかった。その理由も、この次元の問題によるものである。

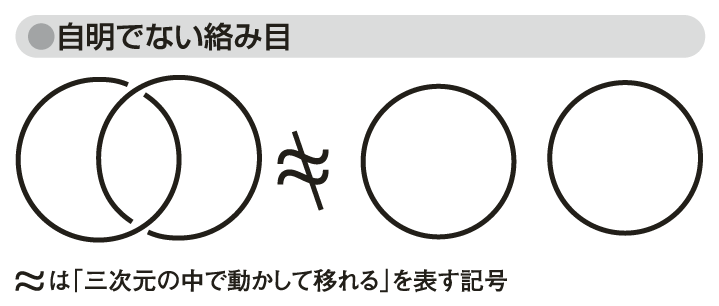
図「自明でない絡み目」

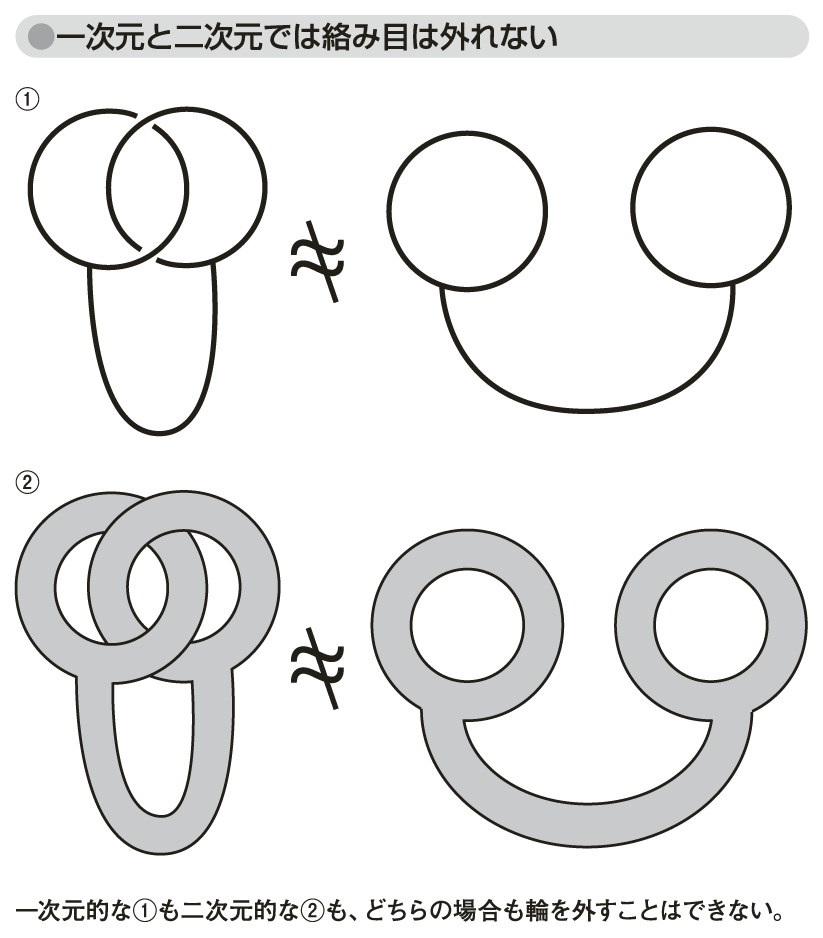
図「一次元と二次元では絡み目は外れない」

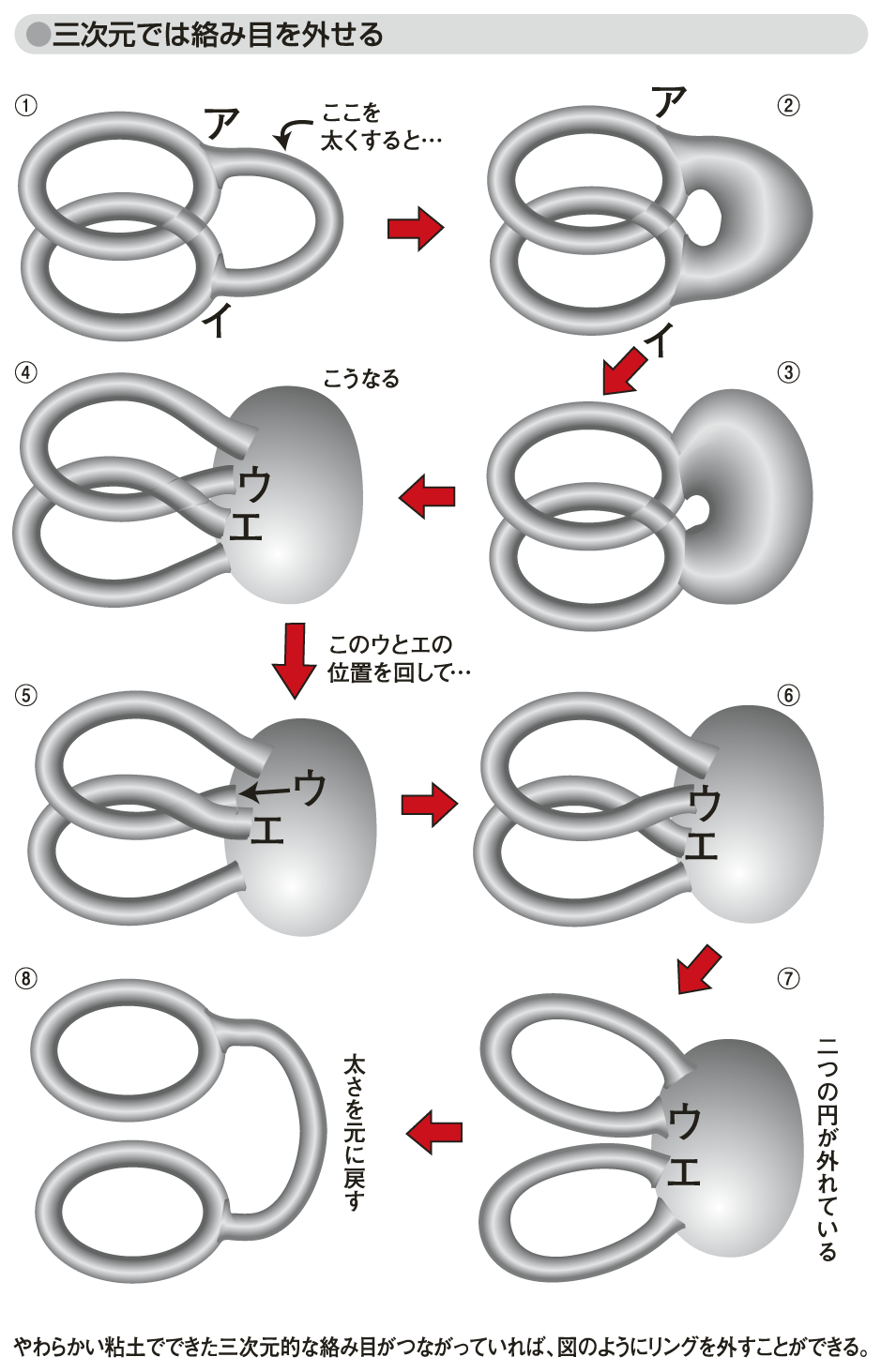
図「三次元では絡み目を外せる」